How to Find Height in a Triangle? Unlock Geometry Secrets

Ever wondered how to find height in a triangle for school or a home project? Understanding this fundamental geometry concept is surprisingly empowering, opening doors to calculating areas, designing structures, and solving real-world challenges. This comprehensive guide breaks down the essential methods, from basic right-angle approaches to more advanced trigonometric techniques, making complex ideas simple and accessible. We explore the what, why, and how of finding triangle height, ensuring you grasp its importance and practical applications. Whether you are a student grappling with homework, a DIY enthusiast, or simply curious about the geometric world around you, mastering how to find height in a triangle is a valuable skill that builds confidence in tackling mathematical problems head-on. This article clarifies common queries and provides actionable steps to ensure you can confidently determine the height of any triangle you encounter.

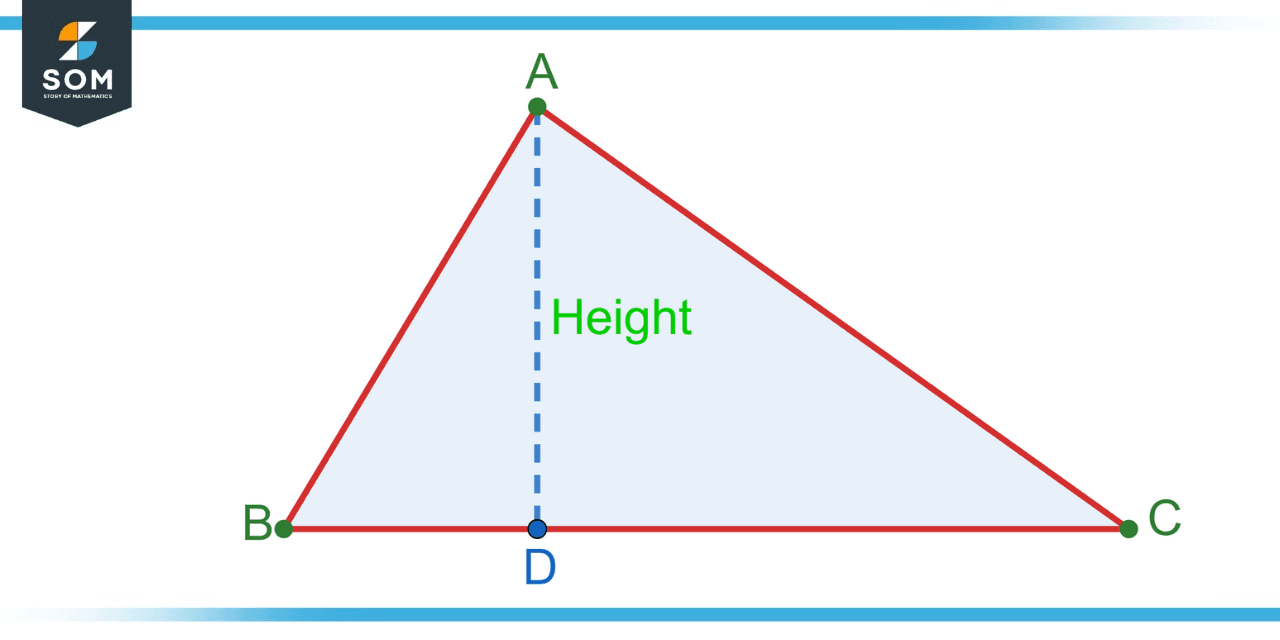
Have you ever looked at a triangular roof or a graphic design element and wondered, How do I find height in a triangle? This question pops up in so many places, from school assignments to engineering projects, because understanding triangle height is a cornerstone of geometry. So, what exactly are we talking about when we discuss how to find height in a triangle? Its simply the perpendicular distance from one vertex (corner) to the opposite side, known as the base. Why is this important? Because knowing the height is absolutely essential for calculating a triangles area, which then helps us with everything from land surveying to architectural design. When do we need this skill? Almost any time youre dealing with shapes, spaces, or structures that incorporate triangles. Where do we use it? Everywhere from classroom problems to building construction sites, even in computer graphics! Who benefits from knowing how to find height in a triangle? Anyone from a curious student to a seasoned engineer can use this foundational knowledge. And how do we actually do it? Well, grab a cup of coffee, and lets explore some incredibly straightforward, yet powerful, methods together to truly master this concept, making geometry feel less daunting and much more empowering.

What Exactly is the Height of a Triangle and Why Does it Matter for How to Find Height in a Triangle?

When we talk about how to find height in a triangle, its crucial to first grasp what the height actually represents. Imagine standing at one of the triangles points, lets call it a vertex. The height, also known as the altitude, is the shortest distance straight down from that vertex to the opposite side, which we call the base. It always forms a perfect 90-degree angle with the base. Why is this specific measurement so important? Well, its primary role is in the calculation of a triangles area. Without the height, figuring out how much space a triangle occupies becomes a guessing game. Think about it: area equals one-half times the base times the height. This simple formula is a workhorse in various fields, allowing architects to determine the surface area of triangular structures, enabling engineers to calculate material needs, and helping artists understand perspective and dimension in their compositions. So, when you learn how to find height in a triangle, youre not just solving a math problem; you are acquiring a fundamental tool that unlocks a deeper understanding of shapes and their practical applications in the world around you. This knowledge empowers you to confidently approach a multitude of problems, making complex spatial reasoning much more manageable and exciting.

The Core Methods: How to Find Height in a Triangle

Now that we appreciate the why, lets dive into the exciting how. Figuring out how to find height in a triangle isnt a one-size-fits-all situation; different triangles and known measurements call for different approaches. But dont worry, each method is logical and builds upon straightforward geometric principles. Were going to break down the most common and effective ways to determine that crucial perpendicular distance, ensuring you have a full toolkit for any triangular challenge. Whether you have the area, certain side lengths, or angles, theres always a path to discovering the height. Understanding these core methods will not only help you solve specific problems but also deepen your overall comprehension of geometry. So, lets confidently explore these techniques, step by step, empowering you to confidently tackle any problem that requires you to find height in a triangle, turning potential confusion into clear, actionable understanding with ease.

Right Triangles: A Straightforward Approach to How to Find Height in a Triangle

When you encounter a right triangle, figuring out how to find height in a triangle becomes refreshingly simple. Remember, a right triangle has one angle that measures exactly 90 degrees. In such a triangle, one of the legs (the sides that form the right angle) can actually serve as the height if the other leg is designated as the base. For instance, if you have a right triangle with legs measuring 3 units and 4 units, and a hypotenuse of 5 units, you could consider the 4-unit side as the base, making the 3-unit side its corresponding height. It’s that direct! However, what if you need to find the height to the hypotenuse? Thats when the famous Pythagorean theorem comes into play, or even the area formula if you already know the area. If you know the two legs, say a and b, and the hypotenuse c, the height (h) to the hypotenuse can be found using the area: Area = (1/2) * a * b. Since Area = (1/2) * c * h, you can set (1/2) * a * b = (1/2) * c * h and solve for h, which simplifies to h = (a * b) / c. This straightforward application demonstrates how knowing how to find height in a triangle for right-angled figures is often less complex than it initially appears, providing a solid foundation for more complex scenarios.

General Triangles Using Area: Unlocking How to Find Height in a Triangle

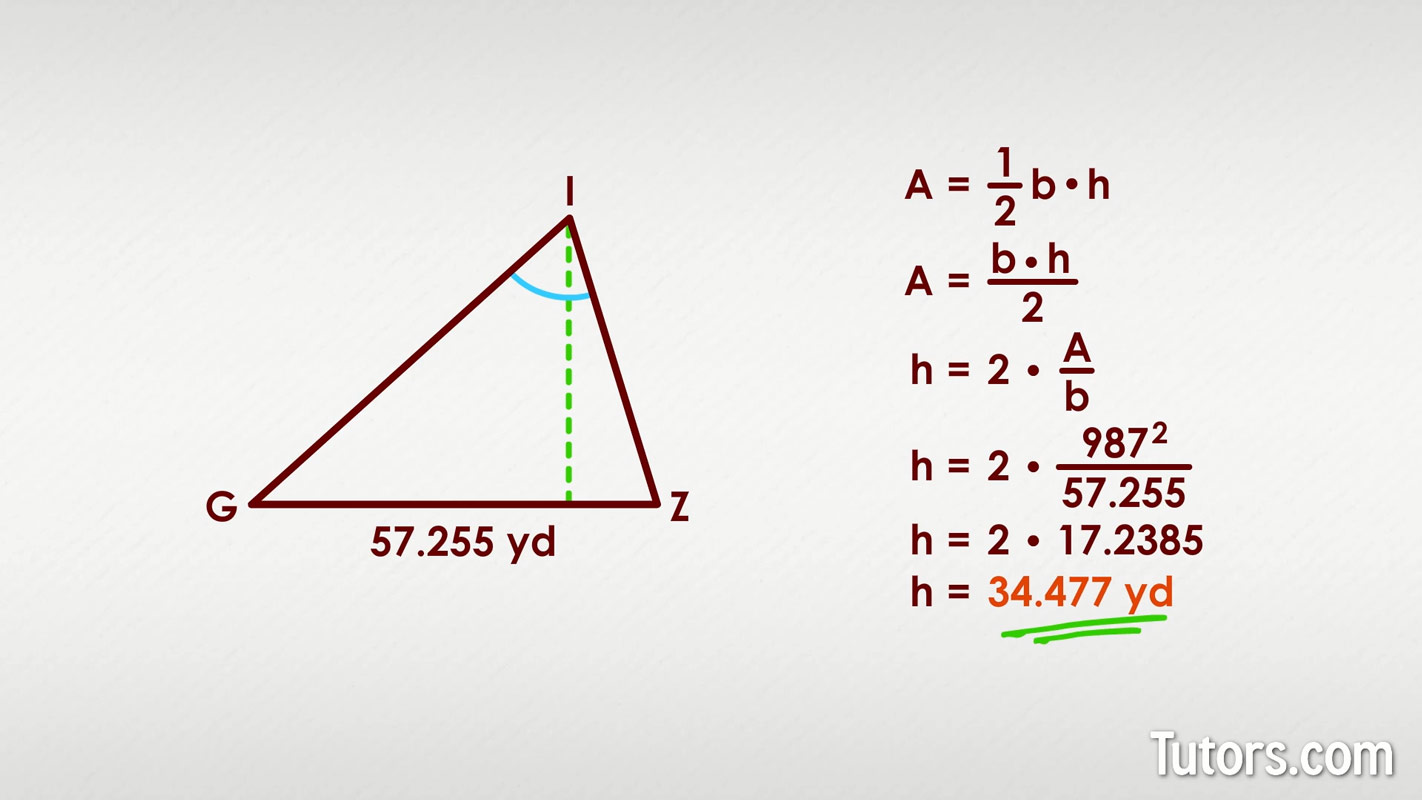
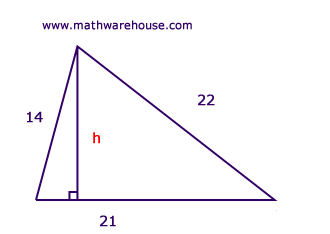
Perhaps the most versatile and widely used method for how to find height in a triangle relies on its area. This approach is fantastic because it works for any type of triangle – acute, obtuse, or right-angled – as long as you know, or can calculate, its area and the length of its base. The fundamental formula for the area of a triangle is: Area = (1/2) * base * height. If you rearrange this formula, you can easily solve for the height (h). Simply multiply the area by two, and then divide by the base length: height = (2 * Area) / base. This makes finding the height incredibly accessible if you have the necessary information. For example, if a triangle has an area of 30 square units and a base of 10 units, its height would be (2 * 30) / 10, which equals 60 / 10, resulting in a height of 6 units. But what if you dont know the area directly? Thats where Herons formula can be a lifesaver. If you know all three side lengths of the triangle (lets call them a, b, and c), you can first calculate the semi-perimeter (s = (a + b + c) / 2) and then use Herons formula to find the area: Area = sqrt(s * (s - a) * (s - b) * (s - c)). Once you have the area from Herons formula, you can plug it right back into our rearranged area formula to determine the height. This shows how knowing how to find height in a triangle can involve a sequence of calculations, each building on the last to reach your ultimate goal.

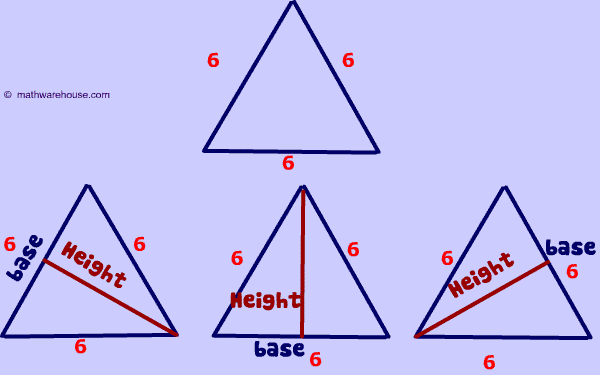
Equilateral Triangles: A Special Case for How to Find Height in a Triangle

Equilateral triangles present a particularly elegant scenario when learning how to find height in a triangle. By definition, all three sides of an equilateral triangle are equal in length, and all three angles are equal, measuring 60 degrees each. When you draw an altitude (the height) from any vertex to the opposite side in an equilateral triangle, it does something special: it bisects (cuts in half) both the angle at the vertex and the base side. This action creates two identical right-angled triangles within the larger equilateral triangle. This is incredibly useful! If you know the side length of the equilateral triangle, lets call it s, then the base of one of these new right triangles is s/2. The hypotenuse of this right triangle is s, and the height h is the unknown leg. Now, we can apply the good old Pythagorean theorem: (s/2)^2 + h^2 = s^2. Lets solve for h. You get s^2/4 + h^2 = s^2. Subtract s^2/4 from both sides: h^2 = s^2 - s^2/4 = (4s^2 - s^2)/4 = 3s^2/4. Finally, take the square root of both sides: h = sqrt(3s^2/4) = (s * sqrt(3)) / 2. This means if you have an equilateral triangle with a side length of 8 units, its height would be (8 * sqrt(3)) / 2, which simplifies to 4 * sqrt(3) units. Isnt it satisfying when specific shapes offer such direct formulas for how to find height in a triangle?

Using Trigonometry: Advanced Techniques for How to Find Height in a Triangle

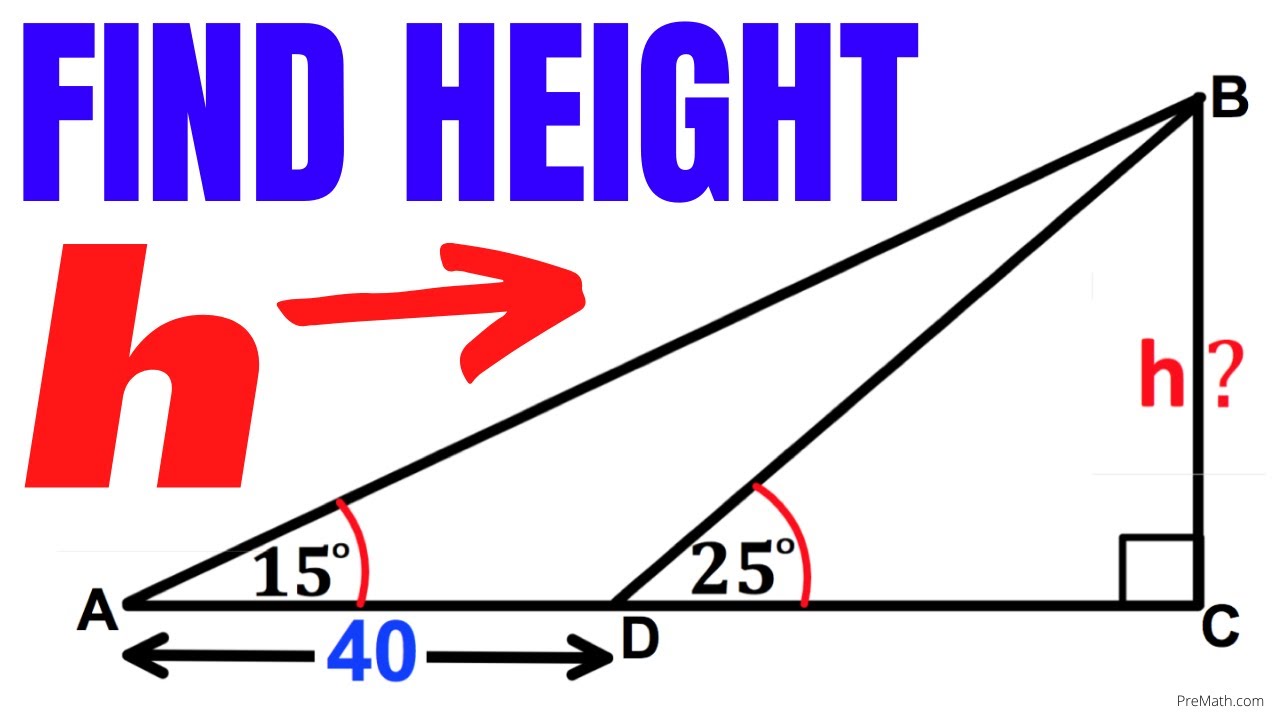
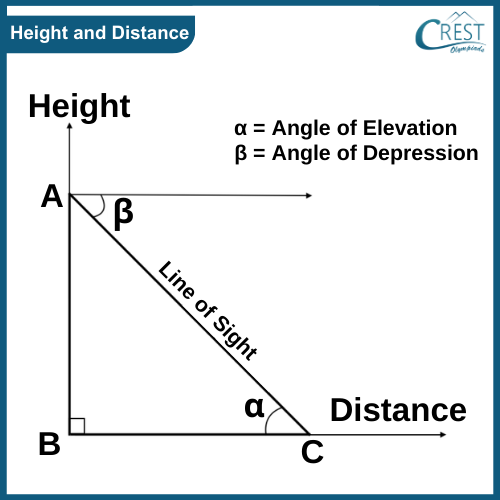
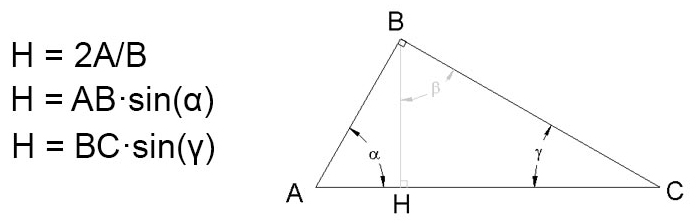
For those times when youre given angles along with side lengths, trigonometry provides powerful methods for how to find height in a triangle. This approach is particularly useful in situations where you might not have the area or all side lengths, but you do have an angle and one or two adjacent sides. The sine function is your best friend here. Recall that in a right-angled triangle, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse (SOH: Sine = Opposite / Hypotenuse). Imagine a general triangle with a base b and an adjacent side a, with an angle θ between a and b. If you drop a perpendicular from the vertex opposite side b down to b, this forms the height h. This height h becomes the side opposite the angle θ in the newly formed right-angled triangle, and side a becomes its hypotenuse. Therefore, sin(θ) = h / a. Rearranging this gives you h = a * sin(θ). This means if you have a triangle where one side is 12 units long, and the angle between that side and the base is 60 degrees, the height to that base would be 12 * sin(60°). Since sin(60°) is approximately 0.866, the height would be roughly 12 * 0.866 = 10.392 units. This elegant trigonometric solution is especially handy in fields like surveying or physics, demonstrating an advanced, yet entirely accessible, way to understand how to find height in a triangle when you have angles at your disposal.

Table: Methods for How to Find Height in a Triangle

Practical Applications: Where Does Knowing How to Find Height in a Triangle Help You?

Beyond the classroom, understanding how to find height in a triangle proves incredibly useful in countless real-world scenarios. It’s not just an abstract mathematical concept; it’s a practical skill that underpins many aspects of our engineered and natural environments. For instance, consider architecture and construction. Architects regularly calculate the height of triangular roof trusses to ensure structural integrity and proper water drainage. Builders rely on these height measurements for cutting materials accurately, minimizing waste, and guaranteeing stability. In surveying, professionals use principles of trigonometry, which includes finding triangle heights, to measure land, map terrain, and determine elevations. Think about a triangular plot of land – to calculate its area for property taxes or development, knowing its height is indispensable. Even in less obvious fields, like graphic design or game development, artists and programmers utilize these geometric calculations to create realistic 3D models and precise spatial relationships. When you learn how to find height in a triangle, you are essentially equipping yourself with a powerful problem-solving tool, one that transforms complex spatial puzzles into manageable, solvable challenges. This foundational knowledge empowers you to look at the world with a more analytical eye, appreciating the hidden geometry that shapes our daily lives and innovations.

Empowering Your Geometry Journey: Mastering How to Find Height in a Triangle

Hopefully, this journey through various methods for how to find height in a triangle has empowered you, revealing that this seemingly complex geometric task is actually quite approachable. We’ve discovered that whether youre working with the simplicity of a right triangle, the general utility of the area formula, the special elegance of an equilateral triangle, or the advanced precision of trigonometry, a clear path exists. Each method offers a unique lens through which to view and conquer the challenge, transforming daunting problems into understandable steps. This isnt just about memorizing formulas; its about building a robust understanding of geometric principles that apply far beyond a textbook. Remember, practice is your best friend here. The more you engage with different types of triangles and apply these techniques, the more intuitive and confident your problem-solving will become. So, keep asking questions, keep exploring, and keep challenging yourself. Youre not just learning math; youre developing critical thinking skills and a deeper appreciation for the structured beauty of the world. Go forth and confidently calculate those heights! What is the primary reason to find a triangles height? To calculate its area, aiding in design and construction projects.

Keywords: calculate triangle height, how to find height in a triangle, triangle area, geometry basics, Pythagorean theorem, trigonometry triangle.

Master various methods for how to find height in a triangle, including using area formulas, the Pythagorean theorem, and trigonometry. Understand the importance of triangle height in real-world applications like construction and design. Learn practical tips and step-by-step guidance to confidently solve height-finding problems. Discover special considerations for different triangle types, such as equilateral and right triangles. Gain a deeper appreciation for the foundational role of geometry in everyday life.

Height And Distance For Class 1 Notes Mental Maths Height And Distance Angle Of Elevation Find The Height H In This Right Triangle Fast How To Find The Height Of A Triangle With Base And Area How To Find The Height Of A Triangle With Base And Area 117x117

Area Of An Equilateral Triangle Formula Equilateral Triangle Height Thora Goodier How To Find Height With Volume And Base Area Aid1667923 V4 728px Find The Area Of An Isosceles Triangle Step 10 Version 2 Equilateral Triangle Side Height Ratio At Dorothy Olin Blog Thora Goodier January 2022 Equilateral Triangle Find Height

Find Height Of Triangle Given Area Step By Step Tutorial With Examples Find Height From Area7 Area Of An Equilateral Triangle Formula Tutors Three Height Lines Equilateral Triangle Geometry Height Find Height From Area 4 Height Of Equilateral Triangle Formula Method FAQs Height Of Equilateral Triangle 1 1636451343

4 Ways To Find The Height Of A Triangle WikiHow Aid1626735 V4 728px Find The Height Of A Triangle Step 7 Version 3 How To Determine The Height Of A Triangle When Given The Area YouTube Heron S Formula To Find Height Of A Triangle YouTube Hqdefault Classifying Triangles By Angles Sides Video Examples Tutors How To Find The Height Of A Triangle Thumb

Height Calculator Angle At Marilyn Tillman Blog Triangle Height Pin How To Calculate Height Of Triangle Find Equilateral Triangle Height Area Of A Triangle Educational Resources K12 Learning Geometry Plane Triangle Height 13245 Calculate Height Triangle At Max Kim Blog Aid1626735 V4 728px Find The Height Of A Triangle Step 9 Version 3

Solving The Height Of A Triangle At A Point Mathematics Stack Exchange HzBZC Triangle Altitude Finder At Harold Mcswain Blog Altitude Of A Triangle Formula Height Of Triangle 696x224 Height Geometry 3 Height Triangle

How To Calculate The Height Of A Triangle Using Heron S Formula YouTube Triangle Height Calculator Inch Calculator Triangle Height Formula Equilateral Triangle Height Area Perimeter Equilateral Triangle Tutors How To Find Height Of A Triangle Example Notes PreAlg 11 01 0006 D 01 20

Equilateral Triangle Definition Examples Formulas Height Of EquilateralHow To Find The Height Of A Triangle YouTube Hqdefault How To Find Height Of A Right Triangle With Hypotenuse And Base At Height Triangle Meaning At Jorge Damon Blog

Height Definition Meaning Height Of Acute Triangle How To Find Height Of A Right Triangle With Hypotenuse And Base At Aid1626735 V4 728px Find The Height Of A Triangle Step 2 Version 3 Unveiling The Secrets Of Triangle Heights A Journey Of Discovery Aid1626735 V4 728px Find The Height Of A Triangle Step 6 Version 3 Geometry Height Area Of Triangles Part1 Image5